Orifice Loss Model
Sharp-Edged Orifice with Different Upstream and Downstream Diameters
The orifice loss factors are all for turbulent Reynolds numbers. The sharp-edged orifice shown in Figure 1, is given by the following (Idelchik 2007Idelchik, I. E., Handbook of Hydraulic Resistance, 4th edition, Begell House, Redding, CT, 2007., 259):
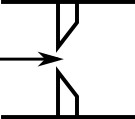
Figure 1: Sharp-edged orifice (in this case Aup = Adown)
Round-Edged Orifice with Different Upstream and Downstream Diameters
When the upstream and downstream pipe diameters are different for a round-edged orifice as shown in Figure 2, the round-edged orifice equation for different pipe areas is used and is given by the following (Idelchik 2007, 258)
where
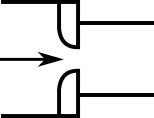
Figure 2: Round-edged orifice with different upstream and downstream pipe areas
Round-Edged Orifice with Identical Upstream and Downstream Diameters
When the upstream and downstream pipe diameters are the same for a round-edged orifice as shown in Figure 3, the round-edged orifice equation for the same pipe areas is used and is given by the following (Idelchik 2007,262)
where

Figure 3: Round-edged orifice with the same upstream and downstream pipe areas
For other orifice configurations, see Chapter 4 of Idelchik's Handbook of Hydraulic Resistance (2007).
Orifice Discharge Coefficient
An alternate method of modeling subsonic pressure loss uses the discharge coefficient. To model this, choose User Specified loss option and the Cd option for Loss Model.
When solving the system, AFT Arrow creates a subsonic CdA for the orifice and solves the pressure drop by iterating the following equation for pressure drop for a given mass flow rate (Keenan 1941Keenan, J.H., Thermodynamics, John Wiley & Sons, Inc., New York, NY, 1941., 317):
where up and down subscripts refer to conditions upstream and downstream of the orifice. In this implementation, the pressures and temperature are static, but the velocity (i.e., Mach number) in the pipe is low compared to the orifice. Therefore, stagnation pressures and temperatures are used. Note that R in this equation is the specific gas constant, which is equivalent to the universal gas constant divided by the molecular weight of the gas in the system.



