Verification Case 11
PRODUCT: AFT Arrow
MODEL FILE: AroVerify11.ARO
REFERENCE: Michel A. Saad, Compressible Fluid Flow, 2nd Edition, Prentice-Hall, Englewood Cliffs, NJ, 1993, Pages 213-215, example 5.2
GAS: Air
ASSUMPTIONS: 1) Adiabatic, 2) Perfect gas
RESULTS:
| Parameter | Saad | AFT Arrow |
| M2 – Mach number at exit | 0.685 | 0.686 |
| M1 – Mach number at inlet | 0.347 | 0.346 |
| P1– Static pressure at inlet (kPa) | 306 | 308 |
| T1– Static temperature at inlet (deg. K) | 312.76 | 312.9 |
DISCUSSION:
As specified, exit conditions are known and inlet conditions need to be determined for specified volume flow at exit. With the known exit conditions, an implied mass flow rate exists. To pose the problem in AFT Arrow terms, a few simple calculations are needed to obtain the mass flow rate. Once obtained, it is applied as a flow demand at the inlet.
The problem states that the exit volume flow rate, Q2, is 1000 m3/min, P2 = 150 kPa, T2 = 293 K. From the ideal gas law, density, and mass flow rate are:
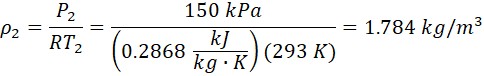
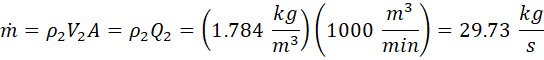
In AFT Arrow, the discharge pressure can be specified. The temperature can be specified at the exit junction, but the actual discharge is what is displayed for the pipe exit. The pipe exit temperature depends on the inlet temperature and the thermodynamic process in the pipe, which is adiabatic. Therefore, to solve this problem the inlet static temperature at J1 must be guessed until the pipe delivers 293 K at the exit. This results in the 312.9 K displayed in the above table.
All results agree closely.
Note that the friction factor in Saad is the Fanning friction factor. To obtain the Darcy-Weisbach friction factor used in AFT Arrow, multiply the Fanning friction factor by 4.



