Transient Flow Equations
To begin with any rigorous fluid dynamics solution, you must start with the most fundamental laws of physics. For isothermal flow of a liquid, there are two core equations - conservation of mass and Newton's second law of motion. We will consider the below control volume in a pipe. The control surfaces 1 and 2 are permitted to move relative to one another, and the unlabeled control surface on the pipe wall must remain fixed to the wall. For the purposes of analyzing a fluid transient, it is safe to consider the system one dimensional in x. Note that there is one radial effect that is important to consider - the change in cross-sectional area of the pipe.
The resulting equations nonlinear hyperbolic partial differential equations, requiring a numeric solution such as the Method of Characteristics.
For a complete development of the equations please see one of the many excellent references (Wylie, et al, 1993Wylie, E.B., V.L. Streeter & L. Suo, Fluid Transients in Systems, Prentice Hall, Englewood Hills, New Jersey, 1993., Chaudhry, 1987Chaudhry, M. H., Applied Hydraulic Transients, 2nd edition, Van Nostrand Reinhold Company, New York, NY, 1987., and Swaffield, et al, 1993Swaffield, J. A., and Boldy, A. P., Pressure Surge in Pipe and Duct Systems, Avebury Technical, Hampshire, England, 1993..
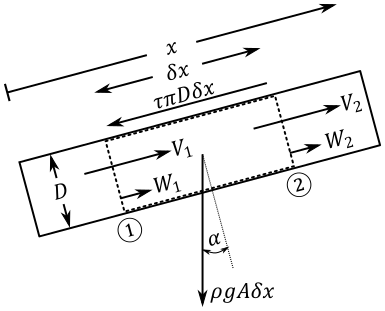
Figure 1: Control volume
Continuity Equation
First we apply conservation of mass to the control volume via Reynold's Transport Theorem:
Simplifying to one dimension:
According to the Leibniz integral rule:
Applying this relationship and canceling terms:
Considering a mean value of the integral:
Divide by δx
Expand and group terms:
This is a generally applicable equation, we have not made any significant assumptions on the nature of the fluid itself.
Next, we will apply the definition of bulk modulus of elasticity. This step carries with it additional assumptions - because we are effectively dropping thermodynamic effects with this substitution, the equation will only be able to be applied to "slightly compressible" fluids. This is not an issue in waterhammer applications - where the fluid is commonly referred to as "incompressible."
Rearranging the above equation, we can find the definition of wavespeed.
Expanding the pressure term, we get a convective term that is typically ignored in waterhammer analysis due to its relatively very small magnitude.
Finally, we arrive at what is termed the continuity equation.
Momentum Equation
The application of Newton's second law follows from the same control volume above. Again applying Reynold's Transport Theorem we begin with the following relationship:
Very similar to the continuity equation, we can apply a one dimensional simplification, the Leibniz integral rule, and consider the resulting integral as a mean over the interval. These steps are extremely similar to the above and are not shown for brevity.
Summing the forces on the body:
To find the shear term, we consider a steady force balance with only two terms - the pressure across a section, and the shear term. We can find the pressure across the section with the Darcy-Weisbach relationship.
Incorporating this, dividing through by δx, and assuming that the areas on the pressure terms can be considered constant, we arrive at the following combined equation:
Expanding the partial derivatives, and dividing through by ρA, we find the continuity equation and can drop those terms. We also again have a convective term which is normally ignored.
Gathering the remaining terms, we arrive at the momentum equation:
Related Topics



