Open vs. Closed Systems
Model a Closed Loop System
A closed circulating system can easily be modeled with AFT xStream by locating a Tank junction anywhere in the system and setting the pressure to the known pressure at that point. Inflow and outflow pipes will then need to be connected. The Tank junction merely acts as a reference pressure against which all other pressures in the system are compared. Because there are no other inlets or outlets to the system, then whatever is delivered by the Tank junction to the system will also be received from the other pipes, thus achieving a net zero outflow rate for the system.
Balancing Mass
In order to model a closed system, only one pressure junction is used in the model. Typically this would be a Tank junction. Pressure type junctions are an infinite source of fluid and do not balance flow. How then can one be used to flow in a closed system?
To answer this question, it is worth considering how AFT xStream views a closed system model. AFT xStream does not directly model closed systems, and in fact does not even realize a closed system is being modeled.
Consider the system shown in Figure 1. This is an open system. Fluid is taken from J1 and delivered to J4 and J5. Because the AFT Arrow Steady solution engine in xStream solves for a mass balance in the system, all flow out of J1 must be delivered to J4 and J5. Because the flow is steady-state, no fluid can be stored in the system; what goes in must go out.
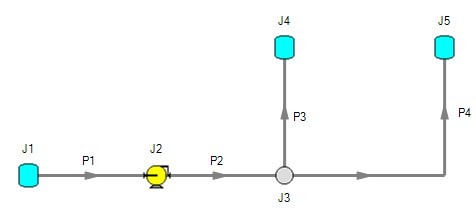
Figure 1: Open system - Flow out of J1 equals the sum of J4 and J5
Now consider the systems in Figure 2. The first system appears to be closed, while the second appears to be open. If the same boundary condition (i.e., pressure, temperature and surface elevation) is used for J1, J11 and J12 in the second system, to AFT xStream it will appear as an identical system to the first system. The reason is that AFT xStream takes the first system and applies the J1 tank pressure as a boundary condition to pipes P4, P9 and P10. The second system uses three tanks to apply boundary conditions to P4, P9 and P10. But if the tanks all have the same pressure, temperature and elevation, the boundary conditions are the same as J1 in the first system. Thus the same boundary condition is used for P4, P9 and P10 in both models, and they appear identical to AFT xStream.
But how is the flow balanced at J1 in the first system? Looking at the first system, one sees that to obtain a system mass balance, whatever flows into P10 must come back through P4 and P9. Because there is overall system mass balance by the solver, it will give the appearance of a balanced flow at the pressure junction J1. If there is only one boundary (i.e., junction) where flow can enter or leave the pipe system, then no flow will enter or leave because there isn’t anywhere for it to go. Thus the net flow rate will be zero at J1 (i.e., it will be balanced). But recognize that AFT xStream is not applying a mass balance to J1 directly. It is merely the result of an overall system mass balance.
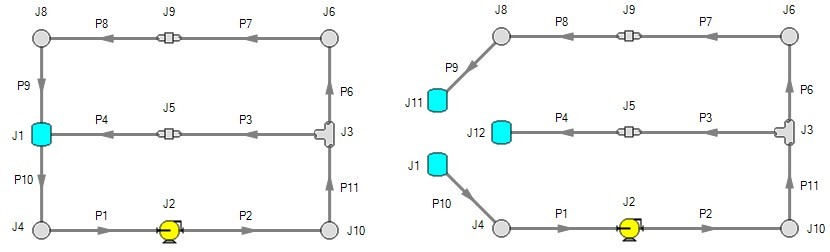
Figure 2: The first system is closed, and the second open. In both systems the flow into P10 is the same as sum of P4 and P9. If the second system has the same conditions at J1, J11 and J12, the two system will appear identical to AFT xStream
Balancing Energy
Consider the system shown in Figure 1. We know that the flows are balanced at J1, but how can the energy be balanced? For example, assume the user sets an initial temperature of 100° F at J1. This temperature will be the inlet pipe stagnation temperature for all pipes that flow out of J1 in the steady state. In this case, the 100° F will apply only to pipe P10.
The pipes flowing into the tank (P4 and P9) will have their own temperatures that are obtained by balancing energy along their individual flow paths. This will include heat exchanger input and heat transfer to or from pipes, as well as any heat of compression effects in the compressor.
The only way to obtain an overall system energy balance is for the J1 tank temperature to adjust to the mixture temperature (mixture stagnation enthalpy, to be more precise) of all inflowing pipes. This can be enforced using the Finite tank option with an Adiabatic Thermodynamic Process. There is a unique “mixture temperature” (or mixture stagnation enthalpy) that will yield an energy balance at J1. This will be the temperature/enthalpy from Equation 49.
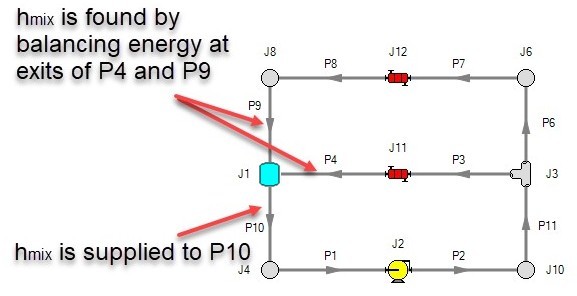
Figure 1: Example of balancing energy in a closed system



