Transient Flow Equations
Any rigorous fluid dynamics solution must start with the most fundamental laws of physics. For fluid flow there are three core equations - conservation of mass, Newton's second law of motion, and conservation of energy. We will consider the below control volume in a pipe. The control surfaces 1 and 2 are permitted to move relative to one another, and the unlabeled control surface on the pipe wall must remain fixed to the wall. For the purposes of analyzing a fluid transient, it is safe to consider the system one-dimensional in the x direction. Note that there is one radial effect that is important to consider - the change in cross-sectional area of the pipe.
The resulting equations are nonlinear hyperbolic partial differential equations, requiring a numeric solution such as the Method of Characteristics.
For a complete development of the equations please see one of the many excellent references (Moody, 1990Moody, Frederick J., Introduction to Unsteady Thermofluid Mechanics, John Wiley & Sons, Inc., New York, NY, 1990. , Wylie, et al, 1993Wylie, E.B., V.L. Streeter & L. Suo, Fluid Transients in Systems, Prentice Hall, Englewood Hills, New Jersey, 1993., Chaudry, 1987Chaudhry, M. H., Applied Hydraulic Transients, 2nd edition, Van Nostrand Reinhold Company, New York, NY, 1987. , and Swaffield, 1993Swaffield, J. A., and Boldy, A. P., Pressure Surge in Pipe and Duct Systems, Avebury Technical, Hampshire, England, 1993. ).
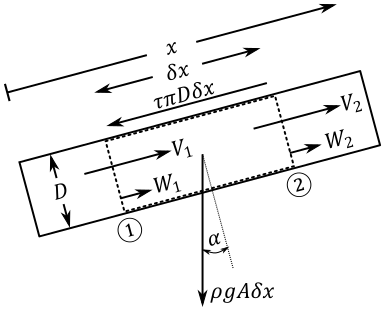
Figure 1: Control volume
Continuity Equation
First we apply conservation of mass to the control volume via Reynold's Transport Theorem:
Simplifying to one dimension:
According to the Leibniz integral rule:
Applying this relationship and canceling terms:
Considering a mean value of the integral:
Divide by δx
Expand and group terms to find the continuity equation:
Momentum Equation
The application of Newton's second law follows from the same control volume above. Again applying Reynold's Transport Theorem we begin with the following relationship:
Very similar to the continuity equation, we can apply a one dimensional simplification, the Leibniz integral rule, and consider the resulting integral as a mean over the interval. These steps are extremely similar to the above and are not shown for brevity.
Summing the forces on the body:
To find the shear term, we consider a steady force balance with only two terms - the pressure across a section, and the shear term. We can find the pressure across the section with the Darcy-Weisbach relationship. Note that this step assumes that the transient shear term can be calculated with an equivalent steady state velocity.
Incorporating this, dividing through by δx, and assuming that the areas on the pressure terms can be considered constant, we arrive at the following combined equation:
Expanding the partial derivatives, and dividing through by ρA, we find the continuity equation and can drop those terms.
Gathering the remaining terms, we arrive at the momentum equation:
Energy Equation
First apply Reynolds Transport Theorem to Newton's first law:
From the First Law of Thermodynamics:
Assuming that the shaft work and viscous work are zero, only the pressure work will contribute as follows:
Combining the three equations above, the surface integrals can be simplified as follows
Simplifying the surface integrals into one dimension, the equation becomes
Dividing through by ∂x, expanding the derivatives and grouping the derivatives results in the following.
To further simplify the above, the continuity equation indicated above can be eliminated. To eliminate the internal energy term use the definition of internal energy and take the partial derivative as follows.
Assuming that gravity and elevation are constant with time, the partial derivative of gz can be dropped. The internal energy derivative can then be substituted into the overall equation.
After expanding the partial derivatives and grouping the common terms results in the following energy equation.
Modified Conservation Equations
The continuity, momentum and energy equations derived above contain a large number of variables which make them unwieldy.
The stagnation and static enthalpy terms in the energy equation can be eliminated using the definition of stagnation enthalpy, the first law of thermodynamics, and various thermodynamic relations and identities. The rearranged energy equation is as follows.
In this form, part of the momentum equation can be inserted into the energy equation. Rearrange the momentum equation as follows. Note that the sin(α) term in the momentum equation shown previously is equivalent to dz/dx.
The rearranged momentum equation can now be inserted into the energy equation to get the Modified Energy Equation:
The continuity equation can be rearranged to insert into the Modified Energy Equation as follows
After inserting the above continuity equation into the Modified Energy equation, multiply through by a2 to find the Modified Continuity Equation as follows
The Modified Continuity and Energy equations can be further simplified by defining the variable F. The final modified equations for F, continuity, energy, and momentum can be seen below in order:



