Discrete and Continuous Sizing
Continuous sizing considers any physical diameter in a given range. The ideal solution of a Continuous sizing will contain fractional sizes. However, piping is generally only available in Discrete sizes - a selection of individual, unique diameters.
It is assumed during a Continuous sizing that the Objective value varies linearly between intermediate sizes. For monetary cost, this is highly unlikely to be the case - custom pipe of unusual diameter would be very expensive. Continuous sizing is useful because it is generally a far easier problem to mathematically solve. On its own, it will give the engineer a good idea of what the ideal system and best-case Objective value looks like. Coupled with a Discrete sizing method, the Continuous sizing result provides an excellent starting point, making the mathematical solution easier.
Continuous sizing methods also generally require less input as they are less restrictive. Starting the sizing process on a Continuous basis is often a good idea at it can reveal potential problems or areas of improvement earlier in the design process.
The selection between Continuous or Discrete is defined on the Sizing Method panel.
Conceptual Example
Our example has so far been a Continuous sizing problem - we are able to select any size of pipe to drive the cost to an absolute minimum. However, the piping is only available in Discrete sizes. This fact will impact the sizing solution and the resulting cost.
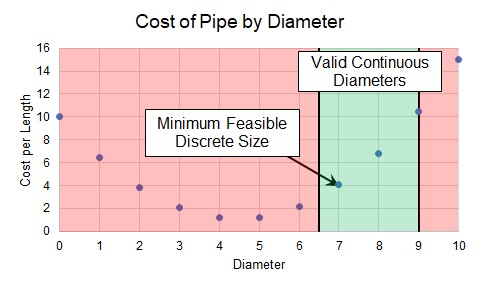
Figure 1: Minimum Feasible Discrete Size
The minimum flow Design Requirement is still considered Active in this case, as it is still driving the sizing solution.
Note: In our example, the cost of diameter "7" is almost double the cost of diameter "6." In such a case, it may warrant further investigation into why the minimum flow rate is required. If the minimum flow was imposed as a rule of thumb or for a non-critical reason, it is well worth considering violating this Design Requirement and selecting size "6" for the cost savings.



