Tolerance Panel
The iterative tolerances that define convergence are defined on the Tolerance panel in Analysis Setup, shown in Figure 1. These values can be modified for Pressure Tolerance, Flow Rate Tolerance, and Temperature Tolerance (when Heat Transfer is enabled).
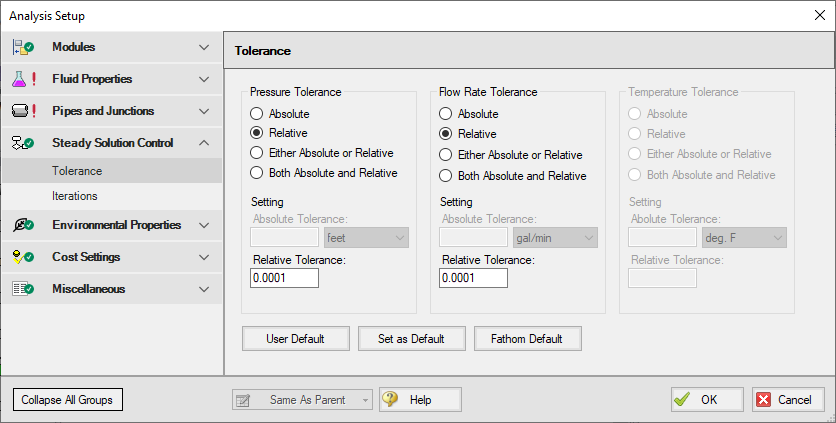
Figure 1: Tolerance panel in Analysis Setup
An iterative approach is used to obtain pipe flow solutions. When approaching any analysis iteratively, a stopping point must be defined. The simplest approach is to stop after a certain number of iterations. However, this either causes uncertain results because the result is still changing, or wasted processing time because there are too many iterations.
A solution is to use iterative tolerance. This tolerance is related to the change between iterations. When this change is smaller than the iterative tolerance, the solution is said to be converged.
Tolerance and Solution Accuracy
Iterative tolerance does not have any relationship to an engineering tolerance.
An engineering tolerance is a familiar term to most engineers - it is a permissible limit in variation of a parameter. A simple example is the length of a steel bar - an engineer might specify that this length must be 3 ± 0.01 meters. A steel bar manufactured by this specification is known to be within the engineering tolerance of the "true" or desired length. In other words, engineering tolerance describes an accuracy.
Iterative tolerances do not directly describe an accuracy. Convergence only means that the change between iterations was within the specified limit.
With sound iterative methods, and an appropriately specified iterative tolerance, the iterative solution will be close to the true solution. However, even with good settings, the iterative tolerance does not define how close the results are to the true solution.
If there is concern that the results may not be close enough to the true answer, the tolerances could be tightened and the results compared. If the results do not change appreciably, an appropriate tolerance was likely selected.
Avoiding False Convergence
It is important to keep the tolerance at least one order of magnitude smaller (two orders or more is recommended) than the relaxation. A false convergence can occur when the change from the old value to the new value is small enough to be within the tolerance because it is restricted by the relaxation.
Absolute Tolerance
Absolute tolerance looks at the absolute change in quantity of a given parameter. If the change is smaller than the directly specified value, the parameter is considered converged.
This approach works equally well for both small and very large values, making iterative solvers more likely to find convergence. However, specifying an appropriate absolute tolerance requires some knowledge of the true solution. The tolerance should be set 3 or 4 orders of magnitude below the solution, if there are near zero flows in the system, this will require a very low tolerance.
Relative Tolerance
Relative tolerance, on the other hand, checks the relative change of a given parameter. Each change is divided by the number itself, giving a change proportional to the magnitude.
This approach does not require any knowledge about the true solution, and for that reason is the default method.
Table 1 shows the difference between relative and absolute change while iterating. Notice that the absolute change has units, while relative change does not.
Convergence criteria can also be based on either (or both) absolute or relative change. Table 1 shows how this is applied.
Table 1: Example of four tolerance methods for a mass flow rate example. Absolute tolerance = 0.0005 lbm/s, Relative tolerance = 0.0001
| Iteration # | Mass Flow Rate (lbm/sec) | Relative Change | Absolute Change (lbm/sec) | Meets Abs. Tolerance? | Meets Rel. Tolerance? | Meets Abs. OR Rel. Tolerance? | Meets Abs. AND Rel. Tolerance? |
|---|---|---|---|---|---|---|---|
| 1 | 20.0000 | - | - | - | - | - | - |
| 2 | 12.0000 | 0.666667 | 8.000000 | NO | NO | NO | NO |
| 3 | 14.0000 | 0.142857 | 2.000000 | NO | NO | NO | NO |
| 4 | 13.5000 | 0.037037 | 0.500000 | NO | NO | NO | NO |
| 5 | 13.6000 | 0.007353 | 0.100000 | NO | NO | NO | NO |
| 6 | 13.5900 | 0.000736 | 0.010000 | NO | NO | NO | NO |
| 7 | 13.5913 | 0.000096 | 0.000130 | NO | YES | YES | NO |
| 8 | 13.5907 | 0.000044 | 0.000600 | NO | YES | YES | NO |
| 9 | 13.5909 | 0.000015 | 0.000200 | YES | YES | YES | YES |
Related Topics
Setting relaxation lower than relative pressure/flow tolerance gives unreliable results.
Related Blogs



