Herschel-Bulkley Model
The Herschel-Bulkley model for non-Newtonian fluids states that the shear rate resulting from a given shear stress applied to the fluid can be described with the following equation:
Where du/dy is the shear rate (or velocity gradient), τ is the applied shear stress, τo is the yield stress, K is the consistency coefficient, and n is the flow behavior index.
The Herschel-Bulkley model describes describes η, the apparent viscosity of the fluid as:
In the Herschel-Bulkley model a value for τo of 0 and a value for n of 1 would result in a Newtonian fluid. The Herschel-Bulkley model is equivalent to the Bingham Plastic model if n = 1, and is equivalent to the Power Law model if τo = 0.
To employ this model, users must have values for τo, K and n, or have rheological data.
Herschel-Bulkley Interface
The Viscosity Model panel appears as shown below in Figure 1 when the Herschel-Bulkley model is selected.
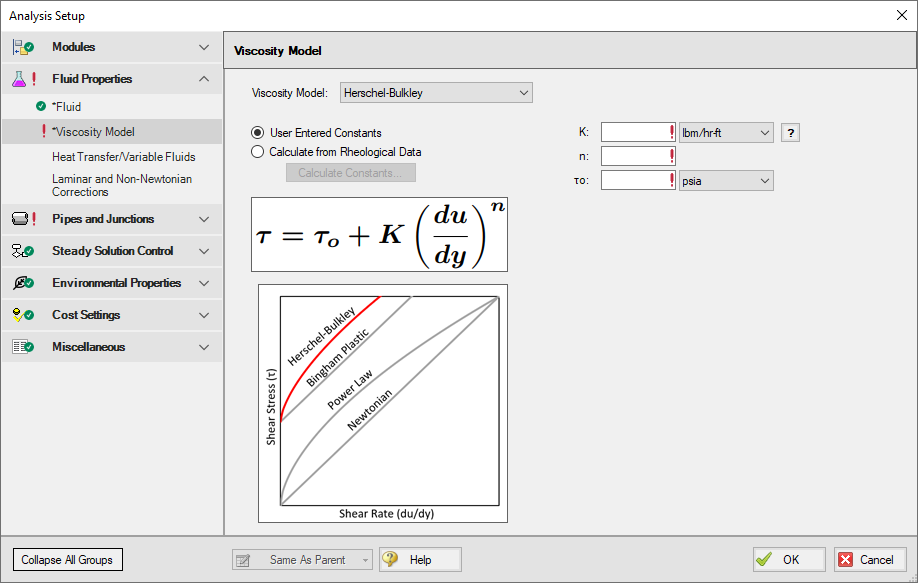
Figure 1: Viscosity Model panel for the Herschel-Bulkley model
Users must enter values for the Herschel-Bulkley constants, K, n, and τo. If the user has raw rheological test data instead, they can enter that directly using the Calculate from Rheological Data option.
Theory and Correlations
AFT Fathom models the frictional losses due to a Herschel-Bulkley fluid using correlations as are summarized in Garcia & SteffeGarcia, E. and Steffe, J., "Comparison of Friction Factor Equations for Non-Newtonian Fluids in Pipe Flow," Journal of Food Process Engineering, Vol. 9, pp. 93-120, April 1986. [Online]. Available: https://doi.org/10.1111/j.1745-4530.1986.tb00120.x (1986). Note that the original equations in the reference use the Fanning friction factor, while AFT software uses the Moody friction factor.
The laminar flow friction factor is defined as
with
and ξo, the dimensionless unsheared plug radius:
The turbulent flow friction factor can be calculated as follows
where
Where He is the Hedstrom number for Herschel-Bulkley fluids and is defined as
Re is the Reynolds number for Herschel-Bulkley fluids, and is equivalent to the Reynolds number for Power Law fluids:
The critical Reynolds number, which represents the transition from laminar to turbulent flow for Herschel Bulkley fluids is defined as
Where n is the flow behavior index, Ψc is equivalent to Ψ with ξo = ξoc, and ξoc is defined implicitly as follows
The friction factor calculated using this correlation is then used to determine pressure loss following Equation 3
in the Network Solution Methodology topic.
These correlations are valid across the full range of Reynolds number. The applicability of this method to highly turbulent flow is limited only by the test data used to determine the Herschel-Bulkley constants.
Curve Fit Methodology
Unlike the Power Law and Bingham Plastic models the Herschel-Bulkley method uses three parameters, so a simple linear regression cannot be used to curve fit all three constants.
Instead Fathom employs the method discussed in Mullineux (2008)Mullineux, G., "Non-linear least squares fitting of coefficients in the Herschel-Bulkley model," Applied Mathematics Modeling, Vol. 32, Issue 12, pp. 2538-2551, Dec. 2008. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S0307904X07002235, which first solves a root-finding equation to determine n, then performs a non-linear regression of τ vs xn to determine the constants K and τo.
The curve fit results using this method have been proven to be identical to the results of a non-linear least squares regression, which is one of the most common methods used to curve fit the Herschel-Bulkley parameters.
If a different curve fitting method is preferable to represent the fluid being modeled the User Entered Constants option should be selected instead.
Related Blogs
Non-Newtonian Fluids - How to Model the Soap, Silly-Putty, or Shampoo in Your Pipe Network
