Power Law Model
The Power Law model for non-Newtonian fluids is one of the most common viscosity models used in hydraulic analysis. This model states that the shear stress required to shear a fluid at a given rate can be described by the following equation:
Where τ is the shear stress, du/dy is the shear rate (or velocity gradient), and K and n are the Power Law constants.
The Power Law model defines η, the apparent viscosity of the fluid as:
In the Power Law model, a value of n=1 corresponds to a Newtonian fluid, while 0 < n < 1 is a Shear Thinning (pseudoplastic) fluid and n > 1 represents a Shear Thickening (dilatant) fluid.
To employ this model, users must have values for K and n, or have rheological test data.
Power Law Interface
The Viscosity Model panel appears as shown below in Figure 1 when the Power Law model is selected.
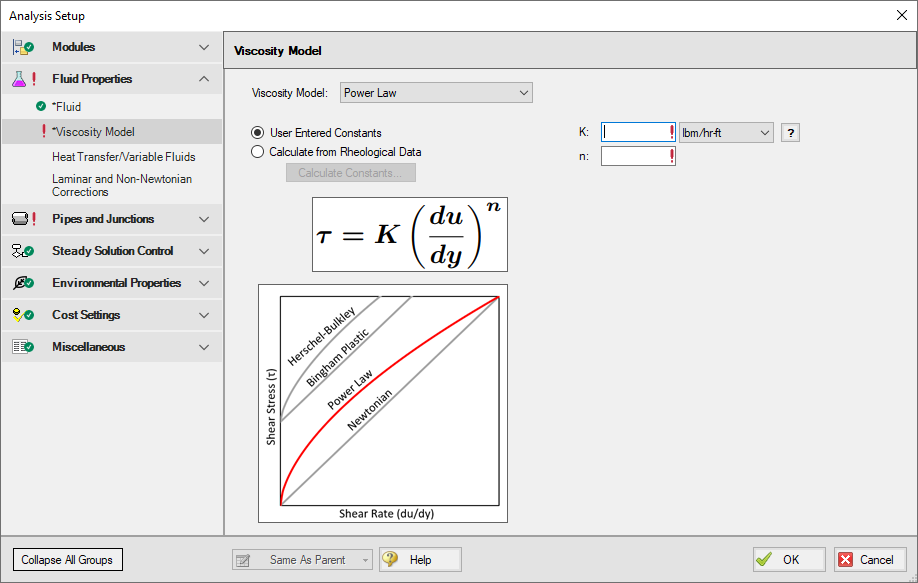
Figure 1: Viscosity Model panel for the Power Law model
Users must enter values for the Power Law constants, K and n. If the user has raw rheological test data instead, they can enter that directly using the Calculate from Rheological Data option.
Theory and Correlations
AFT Fathom models the frictional losses due to a Power Law fluid using correlations taken from DarbyDarby, R., Chemical Engineering Fluid Mechanics, 2nd edition, Marcel Dekker, New York, NY, 2001. , pg. 166-167. Note that the original equations in Darby use the Fanning friction factor, while AFT software uses the Moody friction factor. The equations below have been modified from the original accordingly.
Where:
The Reynolds number for power law fluid (Repl) is defined as:
The critical Reynolds number for power law fluid (Replc) where laminar flow ceases is defined as:
The friction factor calculated using this correlation is then used to determine pressure loss following Equation 3 in the Network Solution Methodology topic.
These correlations are valid across the full range of Reynolds number. The applicability of this method to highly turbulent flow is limited only by the test data used to determine the Power Law constants.
Related Topics
Duffy Method (Pulp and Paper Stock)
Brecht & Heller Method (Pulp and Paper Stock)
Related Examples



