Verification Case 1
PRODUCT: xStream
TITLE: XtrVerify1.xtr
REFERENCE: Gary Sod. A Survey of Several Finite Difference Methods for Systems of Nonlinear Hyperbolic Conservation Laws. Journal of Computational Physics, Elsevier, 1978, 27 (1), pp.1-31, Fig. 4. ff10.1016/0021- 9991(78)90023-2. hal-01635155 (https://hal.archives-ouvertes.fr/hal-01635155/document)
FLUID: Air
ASSUMPTIONS: Calorically perfect gas, ideal gas
RESULTS:
Note: The xStream Standard library fluid for air was updated in xStream 3, which may cause some results to differ from those obtained in previous versions.
DISCUSSION:
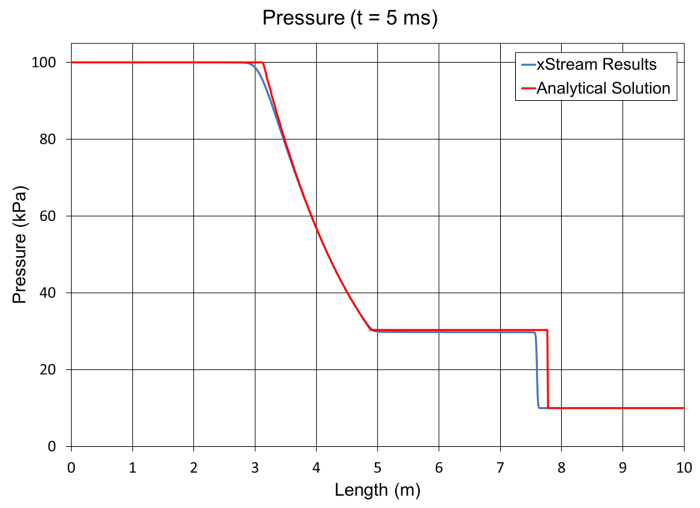
The shock tube apparatus studied for this problem involves a high pressure and low pressure region initially separated by a diaphragm. The high pressure region (x = 0 to x = 5) is initially fully enclosed with a dead end at x = 0. The low pressure region has an open end at x = 10. Both regions are initially at rest. At the beginning of the transient the diaphragm is broken, resulting in a compression wave forming at the broken diaphragm and propagating out from that point. In xStream the initial conditions at the dead end for the high pressure region are modeled using an assigned pressure junction. Since the simulation ends before the wave reflects this is reasonable, but would not be an accurate way to model the dead end for a longer simulation. The diaphragm is represented by a valve which is closed at time 0, then opens instantaneously once the transient begins to represent the diaphragm bursting open.
An analytical solution to this problem can be found by making several simplifying assumptions, including that the pipes are adiabatic and frictionless, and that the gas is calorically perfect and ideal. This means that the fundamental compressible flow equations can be solved assuming flow is isentropic, except at the shock wave. The analytical solution was calculated using the basic equations as are described on page 3, along with the fundamental compressible flow equations.
The initial values for pressure and temperature were chosen in order to satisfy the pressure and density ratios specified by the reference for the steady state.
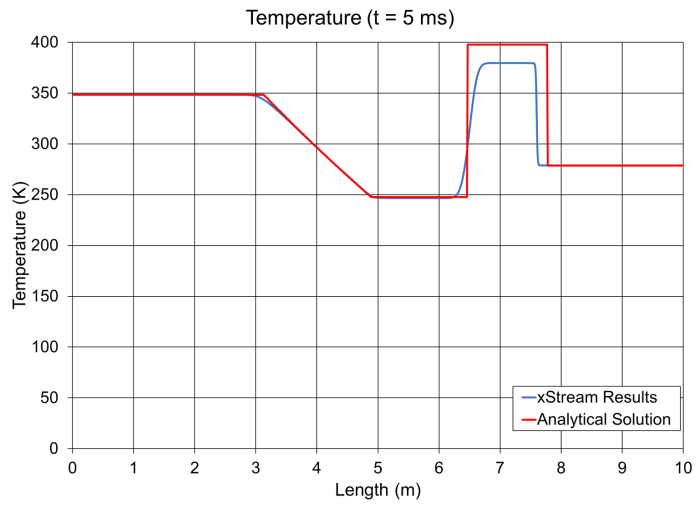
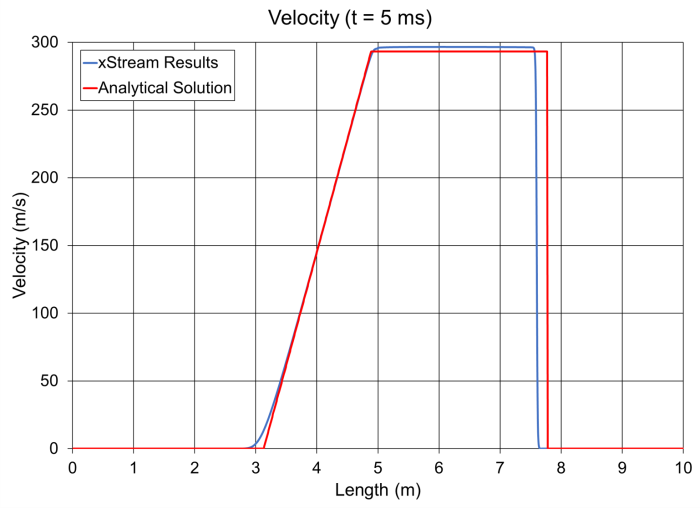
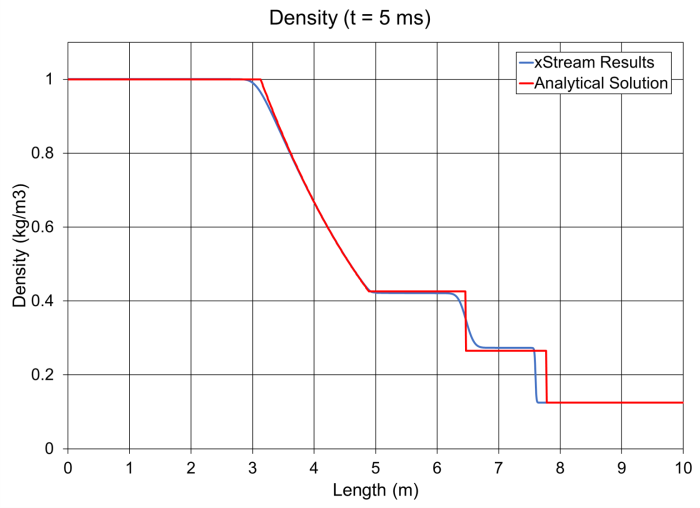
It can be seen that the relative magnitudes of the pressure, density, and velocity are reasonably close to the analytical solution, though the shock wave front is shifted slightly to the left. There is a more noticeable difference in the maximum temperature results for xStream and the analytical solution, though the margin of error is still relatively small. The lower temperature predicted by xStream will also cause a lower sonic velocity for the fluid, which explains the shift in the shock wave front.