Network Implementation
To provide converged solutions in the shortest time possible, matrix solution techniques are used. Matrix techniques allow all pipes to be solved simultaneously, which is faster and offers the best convergence characteristics.
To obtain a valid solution in a network, the stagnation pressure at each branch point must be equal. Additionally, the mass flow, energy flow, and species concentrations must sum to zero at the branch. Although the stagnation pressures at the pipe endpoints will equal that at the connecting junction, this is not true for stagnation enthalpy (and temperature). The stagnation enthalpy at the end of a pipe will be that enthalpy that results from the heat transfer in the pipe. Once the fluid flows into the junction, the stagnation enthalpy will change to the mixture stagnation enthalpy, or the average stagnation enthalpy of all inflowing pipes.
If only one pipe flows into the branch, the branch stagnation enthalpy will equal the stagnation enthalpy coming out of the pipe. But if more than one pipe flows into the branch, the stagnation enthalpy will reach an averaged condition. It is this averaged stagnation enthalpy that results from mixing two or more streams at different stagnation enthalpies. This stagnation enthalpy is supplied to all outflowing pipes. This is depicted in Figure 1 and follows Equation 49.
|
|
(49) |
where the + superscript indicates the summation applies only to positive inflows into the junction.
The concentration balance at a junction is similar to stagnation enthalpy. The junction concentration itself will not match the concentrations for the inflowing pipes, but will be a mixture of the incoming flow streams.
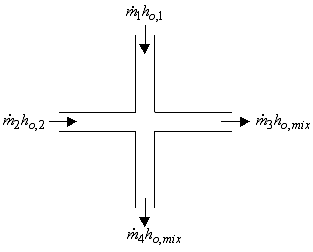
Figure 1: Flow weighted mixing and energy balance



