Gradient Based Methods
Gradient based methods search for the ideal solution using the gradient of the Objective Function. A gradient is a vector function composed of partial derivatives measuring the change of some function with respect to each component. Effectively, a gradient is a derivative of a multi-variable function - it indicates the magnitude and direction of greatest change in a multi-variable function.
A gradient of a single variable function is simply the derivative of that function. While most problems requiring complex optimization techniques have many variables, it is easiest to think about a single-variable function, such as elevation related only to distance along some horizontal line:
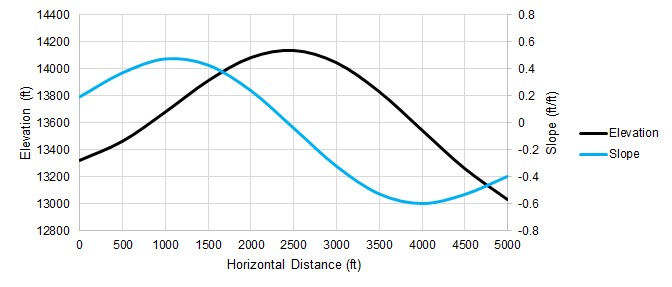
Figure 1: One of many possible elevation profiles of a mountain peak. The slope can be calculated at any point.
The gradient of a mountain's elevation will indicate the magnitude and direction of the elevation change at any given latitude and longitude. In other words, given a specific point, the gradient will tell you how steep the slope is at that point, and which direction it is steepest in. This is very useful for finding the top of the mountain - without being able to see anything but the local value of the gradient, you can make an estimate that the peak is probably in the direction of the slope, and that if the slope is very steep you likely have a long ways to go.
If the entire elevation profile was known ahead of time, finding the peak is trivial. Unfortunately, we do not normally know the entire profile, but instead can only determine its value where we explicitly test it. Stated generally, the shape and behavior of an Objective Function is not known ahead of time.
Rather than testing every single horizontal point to find the highest elevation by brute force, we can an employ an intelligent gradient based search method. Starting at a horizontal distance of zero, we can measure an elevation and slope:
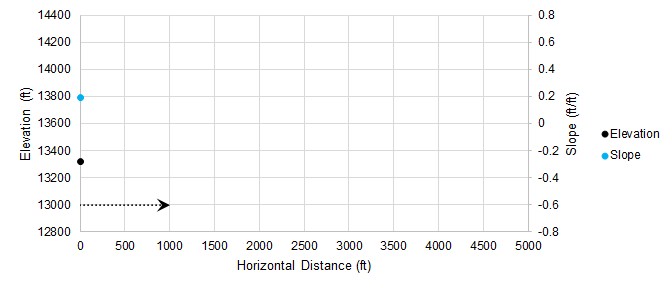
Figure 2: Starting a gradient based search
With the positive slope from our initial condition, we can make an educated guess that the peak is somewhere in the positive direction. We determine where we want to guess and measure our system again at that point:
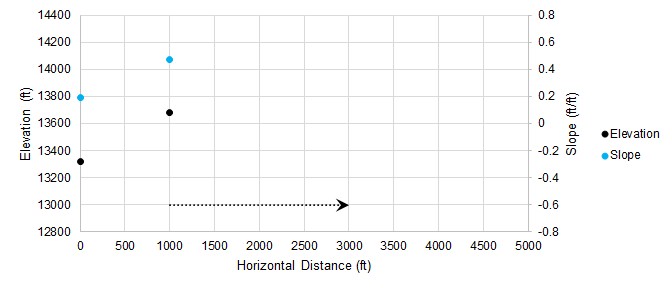
Figure 3: Iteration number 2
Because our slope is higher, we assume that the peak is farther away and adjust our change in distance accordingly. Our new guess has a negative slope, so we will reverse our search direction.
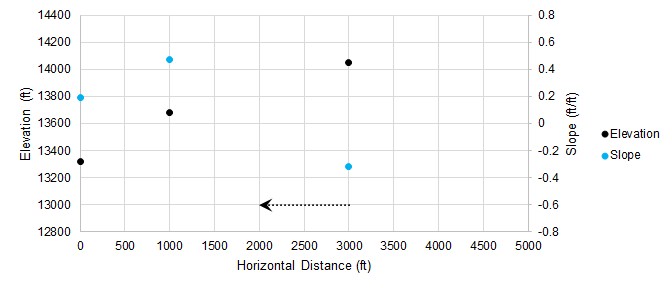
Figure 4: Iteration number 3
We changed sign on slope again, so we reverse direction again. We can use information from previous guesses to narrow down the search range and make a more intelligent guess.
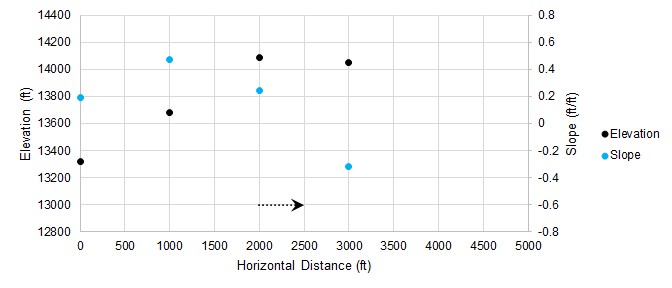
Figure 5: Iteration number 4
As we continue, the adjustments to our guess get smaller and smaller. Once they are small enough, we can consider the search converged, and the peak found.
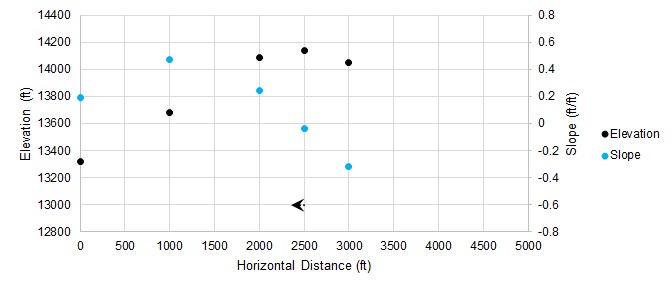
Figure 6: Iteration number 5
In only a few iterations, we have found an excellent approximation of the highest point, without knowing anything about the elevation or slope outside of our selected guess points.
The search algorithms included in ANS are much more sophisticated than the simple example presented here, but the idea remains the same. Furthermore, the allowable selections are restricted by Design Requirements, which impacts the ideal search direction.



